
The ages of the people in the sample are shown in column A of the worksheet in Figure 1. ExamplesĮxample 1: A random sample of 12 people is taken from a large population. Based on Table 2 of the Shapiro-Wilk Tables the p-value for the test is somewhere between. This is the p-value for the test.įor example, suppose W =. Find the value in Table 2 of the Shapiro-Wilk Tables (for a given value of n) that is closest to W, interpolating if necessary.Calculate the test statistic W = b 2 ⁄ SS.Calculate b as follows, taking the a i weights from Table 1 (based on the value of n) in the Shapiro-Wilk Tables. Note that if n is odd, the median data value is not used in the calculation of b.If n is even, let m = n/2, while if n is odd let m = ( n–1)/2.Arrange the data in ascending order so that x 1≤ … ≤ x n.The basic approach used in the Shapiro-Wilk (SW) test for normality is as follows: Royston which can handle samples with up to 5,000 (or even more).
By clicking here you can also review a revised approach using the algorithm of J.

This approach is limited to samples between 3 and 50 elements.
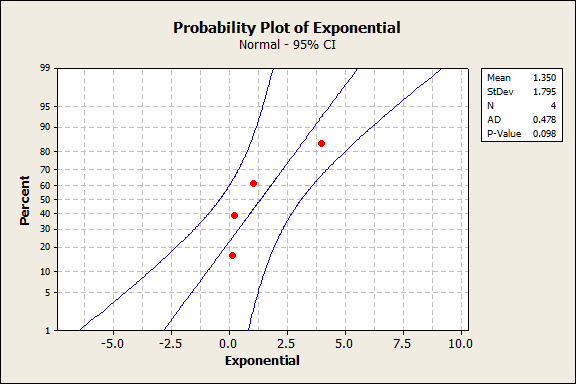
We present the original approach to performing the Shapiro-Wilk Test.


 0 kommentar(er)
0 kommentar(er)
